1. My resolution of the Russell paradox
My resolution of the Russel paradox is, simply put, that no class is, or can ever be, a member of itself. Self-membership is unconscionable. It is therefore no surprise that the unthinking adoption of the idea of self-membership by Russell led him to paradox. The concept of class-membership differs significantly from that of predication. Predication is a natural way of thinking; class-membership is an artificial one, invented by logicians. The concept of class-membership is useful, but it has limitations. The idea of class-membership is very early, being implied already in Aristotle’s discourses; but became more consciously used by logicians in modern times.
The original idea is that if any individual thing (call it X) ‘has’ some property (call it Y-ness), then it is ‘subsumed’ under the species or genus of Y-having things; i.e. if X is Y, then X is a Y (notice the use of ‘a’ to signal that a species or genus, as distinct from a property, is intended by Y). This thought later led to the idea of a ‘class with members’, defined by: if X is a Y, then X is a member of the class “Y” (notice the use of inverted commas to refer to a class as distinct from a predicate). Tacitly intended here are the complements: “if X is not Y, then X is not a Y” and “if X is not a Y, then X is not a member of the class ‘Y’,” note.
But it should be made clear that these two ideas, though related, are quite distinct. While it can be said of anything which is Y, that it is a Y; it cannot be said of any class “Y” which happens to be a Y, that it is a member of the class “Y” (i.e. a member of itself). For the idea of class-membership is figuratively the idea of an enclosure (the class) in which a group of things (the members) that are alike in some way (i.e. have some property in common, say Y) are included; and it is impossible to visually imagine that the enclosure will be included within itself (i.e. that the class can be a member of itself). One can say it in words, of course; but one cannot draw it on paper.
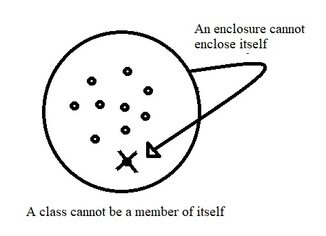
Thus, the idea of subsumption under a species or genus (of “Y” under Y) and that of class-membership (of “Y” in “Y”) are only partly equivalent, and should not be confused. For example, whereas the class “classes” is indeed a class, it cannot logically be a member of the class “classes.” The characterizations “is a class” and “is a member of the class ‘classes’” are not interchangeable. The class “classes” can, however, still be a member of other classes, notably of the class “not self-member classes.” Indeed, no class can be a member of “self-member classes,” because there is no such class (as just explained); and consequently, all classes are members of “not self-member classes.”
Note this well: even though some classes (such as the class “classes”) do subsume themselves, they cannot reasonably be said to be members of themselves. This signifies that, whatever the value of Y: whether the class “Y” is or is not a Y, “Y” is not a member of the class “Y,” i.e. it is not a member of itself. So, the proposition through which we initially defined class-membership, viz. if X is a Y, then X is a member of the class “Y,” has a formal exception, viz. the case where the class “Y” is intended by the term X (which is otherwise general).
(Although we have not here dealt with subclasses and overclasses, note that the said exception does not prevent the class “Y” from being a member of the overclass “Y-classes;” which, by definition, includes “Y” together with all the subclasses of “Y.” This is true because “Y” and “Y-classes” are at different levels, so this does not constitute self-membership. More on this below.)
Another oddity of class logic to note is that, just as “classes” is a class, “non-classes” can be said to be a class, without self-contradiction. In the case of predicate logic, such a twist is not possible; i.e. a non-class (i.e. a thing that is not a class) cannot be said to be a class: only a class can be said to be a class. This again proves the divergence between these two ways of thinking. On the other hand, note, “classes” cannot consistently be said to be a non-class; and likewise, “non-classes” cannot be said to be a non-class.
As regards the Russell paradox, it is alleged that the class of “all classes not member of themselves” constitutes a double paradox, because: if we say it is not a member of itself, then it is a member of itself, and if we say that it is a member of itself then it is not a member of itself. But it is clear, in the light of what we have realized above, that the problem lies in the consequent of the first if-then statement and in the antecedent of the second if-then statement, i.e. in the false claim that they contain that “all classes not member of themselves” can be a member of itself. In truth, no class is a member of itself, so both the if-then statement made are wrong (non-sequiturs).
In other words, the resolution of Russell’s paradox is that the class “all classes not member of themselves,” just like any and every other class, is not a member of itself, and this claim does not give rise to any self-contradiction.
2. Why Russell’s resolutions are inadequate
Now, Bertrand Russell did formulate a somewhat similar explanation of his paradox, saying:
“No collection (whole or totality) can contain members that are defined in terms of itself; specifically, no existing collection can ever be a constitutive part of itself”[1].
How does this formulation differ from my denial of the logical possibility of self-membership? Russell’s formulation obviously refers indirectly to the collection itself; i.e. he means, more directly put: a collection cannot contain itself as a member because such membership could only be triggered by defining the collection in terms of itself, and that is not feasible. Where is the “definition,” here? It is the term’s formulation itself, viz. “all classes that are members of themselves” in our case.
The proposed definition involves the term that is being defined; i.e. there is an element of self-reference, of circularity. This can be called self-definition; and it is obviously useless, if we do not already know what is intended by other means. But is definition of the class in terms of itself the issue at hand, here? I would say not: this term is merely the end-product of a reasoning process; it does not suddenly come out of the blue. It is this reasoning process that needs to be examined and evaluated.
Is the class of “all classes that are members of themselves” produced by self-definition? No – the underlying predicative term “all classes that are classes” is not problematic: indeed, all classes are classes. This predication engenders the classificatory term “all classes that are members of ‘classes’,” which is not per se problematic, either. What is problematic is that the latter term, using for example the fact that “classes” is a class, and so apparently a member of itself, inductively gives rise to the term “classes that are members of themselves.” So, the genesis of the latter, problematic term is not through mere self-definition, as Russell seems to think, but through the illegitimate traduction (putative translation) of a perfectly legitimate predication into a class-membership proposition.
The said traduction is known and proved to be illegitimate by the fact that it gives rise to the Russell paradox. My proposed resolution is easily proved with reference to the negative term “all classes that are not members of themselves.” If the issue were self-definition, as Russell suggests, then this term too would be problematic, since it also refers to itself (if only negatively); yet this term is not problematic![2] Clearly, then, the issue at hand is not self-definition, but something else entirely. It is the naïve inference just described.
More accurate is Russell’s concluding statement, viz. that “no existing collection can ever be a constitutive part of itself” – but that is not an explanation in itself: it is an evident consequent of the Russell paradox, i.e. a statement that there is obviously some sort of problem with any “existing collection” being “a constitutive part of itself,” which implies that such a collection cannot exist. That is not an explanation, but an observation needing an explanation, and the explanation Russell offers revolves around self-definition, as we have seen. But self-definition is not, in fact, genetically involved.
I would say that, although Russell glimpsed that there is a problem inherent in the idea of self-membership (or, alternatively, perhaps, that of non-self-membership) by a class, he did not correctly understand precisely why the problem arose. He wrongly identified the problem as self-definition, i.e. as self-reference in definition. But though this feature is present and significant, it is not the crux of the problem.
In truth, the problem can only be solved through the finer conceptual analysis I have formulated. The problem arises through the assumption that subsumption under a concept and class-membership are fully parallel (effectively interchangeable) ideas – they simply are not. It is this prior faulty assumption which eventually gives rise to the Russell paradox. Once this is understood, it is easy to see why “self-membership” is unconscionable and we must say categorically that no classes are members of themselves, and in that event no Russell paradox arises anymore.
Later on, Russell, seemingly dissatisfied with his earlier proposed resolution of his double paradox, proposed his Theory of Types as a means to this end. In its simplest form, this theory focuses on the differences between the individual items subsumed by classes, the classes themselves, the classes of classes that the latter are subsumed by, and so on. These are successive “types,” forming a hierarchy of items from the concrete objects to more and more abstract derivatives of them.[3]
Very briefly put, the theory postulates that a proposition may be universally true of a lower type, but not include a higher type. For example, all classes can be said to be members of the class “classes,” without this implying that “classes” is also a member, simply because (the theory claims) it is of a higher type than all the classes it includes. So, “all classes” does not literally mean all classes; it can (due to “type” difference) exclude the class “classes” itself. Of course, this claim is quite arbitrary, and merely conceals the Russell paradox behind a smoke screen.[4]
There is some truth to this idea, but it also involves some confusion. There indeed exists a hierarchy between concrete individual items, abstract groupings of items (classes), and more abstract groups of groups of items (classes of classes). However, the Russell paradox does not arise when we try to include a class in a class of classes, i.e. a subclass in an overclass. And of course, the Russell paradox does not arise when we try to include an individual item in a class. The Russell paradox only arises when we try to include a class in itself; or (by extension) a class of classes in itself.
The Russell paradox only arises in attempts to self-include a class, or a class of classes, in itself. So, hierarchy is not the issue, here, and the theory of types cannot provide a solution! It is only incidentally true that a class can only group concrete objects, or a class of classes can only group less abstract classes. The reason for the paradox is not type differences, but the fact that a class or class of classes cannot, even in imagination, include itself in itself.
Note in passing that, in our above example, the class “classes” (i.e. the class of all classes) is really a class of classes, since the units it groups are all classes. Nevertheless, it remains a class in its own right, and as such apparently belongs under itself, i.e. subsumes itself. The solution is not that it cannot subsume itself, but only that it cannot be a member of itself. This is not a matter of hierarchy (type), but a matter of changing predication into classification.
3. Why Rescher’s resolution is inadequate
Nicholas Rescher’s proposed resolution of the Russell paradox is somewhat but not much different from Russell’s first attempt. He applies a general principle that he has formulated, called the Successful Introduction Principle, to the case at hand. He points out that “only when something is properly identified, can it serve as a subject of meaningful discussion;” adding: “With an inappropriately identified pseudo-object… the door to contradiction and paradox is thrown wide open”[5]. In his view, then, the Russell paradox is caused by a failure of proper identification inherent in a class defined in terms of itself.
Thus, Rescher focuses on the problem of self-definition, just as Russell does. His approach differs, as he points out, in that whereas Russell sees self-definition as an ontological issue, Rescher sees it as a communicative issue. For Russell a class cannot exist which is defined with reference to itself; whereas for Rescher, we cannot even begin to use or discuss such a class, because it is as if nothing has been said yet. Both these insights are, in my view, true. But they do not resolve the Russell paradox, as already explained. To repeat, the issue is not one of self-definition, but of passing over from a predicative discourse to a classificatory one. A class like “classes” is indeed a class, but “classes” cannot be a member of the class “classes.” These are two different systems of thought, which do not behave identically in all circumstances.
We cannot form concepts at will, just by putting some words together in a definition. A definition is a hypothesis subject to verification by logic. In the case of the definition of class-membership, viz. the proposition that “if X is a Y, then X is a member of the class ‘Y’,” double paradox is found to ensue in the special case of “if ‘Y’ is a Y, then ‘Y’ is a member of ‘Y’.” Therefore, the rule we tried to formulate (i.e. the said definition of class-membership) must have an exception; namely, when X stands for the class “Y.”
The Russell paradox is valuable in that it teaches us that an exception must be allowed for in the defining formula. We initially assume the general definition to be valid; but after we find out that it leads to self-contradiction and paradox, we are obliged to retract it in part. We are logically forced to altogether reject the notion of self-membership. This is a very limited and precise retraction, but it restores consistency to class logic. Our hypothetical definition has been adjusted to avoid inconsistency. This is the correct resolution of the Russell paradox.
4. Other incarnations of the paradox
It should be mentioned that Russell realized that the concept of class was at issue somehow, but then he tried to show that the same paradox could be formulated within predication. As Kneale and Kneale rendered it[6]:
“Instead of the class which is supposed to contain all classes that are not members of themselves let us consider the property of being a property which does not exemplify itself. If this property exemplifies itself, then it cannot exemplify itself; and if it does not exemplify itself, then it must exemplify itself. Clearly, the nature of the trouble is the same here as in the original paradox, and yet there is no talk of classes.”
The implications here are that some properties “exemplify” themselves, while some do not. That is, a property Y: in some cases, Y is Y (i.e. has property Y) and in others Y is not Y (i.e. lacks property Y). If Y is Y, then Y exemplifies itself; and if Y is not Y, then Y does not exemplify itself. Is it, however, ever true that Y is Y? Can anything be pointed to that has precisely itself as a predicate? I would say not. Clearly, ‘Y is Y’ here does not refer to a predicative tautology, like ‘white is white’. Rather what we mean by ‘Y is Y’ here is that ‘whiteness is white’, i.e. Y-ness (the property Y) is Y (has the property Y). This is a very different statement, which does not follow from the preceding one.
And the same critique of it can be brought to bear for it as for the classificatory version. We may well say that if X is Y, then X “exemplifies” Y-ness (i.e. is one of the things that has Y-ness), but in the special case where X is replaced by Y-ness (i.e. the property Y), we must make an exception, and deny that ‘Y-ness is Y’ implies ‘Y-ness exemplifies Y-ness (i.e. itself)’. To avoid an eventual Russell paradox, we must at least short-circuit such implication, if not totally reject the consequent (saying that it is never true that Y-ness exemplifies Y-ness), if not even reject the antecedent (saying that it is never true that Y-ness is Y).
Russell claimed that if “the property of non-self-exemplification” exemplifies itself, then it lacks “the property of non-self-exemplification” and so cannot exemplify itself; and if does not exemplify itself, then it has “the property of non-self-exemplification” and so must exemplify itself. To my mind, this means we must reject the very idea of self-exemplification and say that nothing exemplifies itself (even if we happen to find some Y-ness which is Y). In that event, we can well say that “the property of non-self-exemplification” does not exemplify itself, without any contradiction arising.
The same thing can be said using other terms: some concepts are “instances” of themselves, while some are not. That is, we can define instantiation by saying: if X is a Y, then X is an instance of Y (i.e. X is an individual within the group called Y); but we must make an exception in the special case where X is replaced by Y, and deny that if Y is a Y then Y is an instance of Y. It is clear that Y here refers specifically to a concept, and not just any kind of thing. An example would be “the concept ‘concept’ is a concept; therefore, the concept ‘concept’ is an instance of itself.”
This is clearly very similar to saying “the class of all classes is itself a class; therefore, the class of all classes is a member of itself;” and a similar paradox is bound to emerge from it, which can be neutralized in a similar manner. That is, we must upon reflection say that nothing is an instance of itself, so that in fact “the concept of non-self-instantiation” is not an instance of itself. A similar line of reasoning can be followed with regard to “inclusion” and any other similar relations.
Clearly, none of these issues relate to predication as such, but to more geometrical ideas (classifying, having/belonging, instantiating, including) through which we try to represent predication. These relations are intended as metaphors for predication; but it turns out that these analogies are not perfect. The lesson the Russell paradox teaches us is that these derivative relations all have exceptions (as already detailed above). The Russell paradox does not affect predication as such; predication as such is immune to it. Although Russell was right to investigate whether his paradox meme affects predication as such, he was wrong to conclude that it does; it does not.
5. About the Barber paradox
There is a town with only one barber. Some men in it shave themselves; the rest do not, but are all shaved by the barber. What about the barber? Does he shave himself or not? If he does, he is one of the men who shave themselves (no problem); if he does not, he is one of those shaved by the barber, i.e. by himself (apparent contradiction). Obviously, in his case, the two classes of men overlap: he both “shaves himself” and he is “shaved by the barber.” This is hardly problematic: it just tells us that the supposed either-or disjunction between the two groups of men is not really one; his case is a logically implied exception to it. That is, in his case, unlike in other cases, being shaved by the barber does not imply not shaving himself.
How does this compare to the Russell paradox, of which the barber paradox is touted as an illustration? I resolve the Russell paradox by saying that no class is a member of itself; it follows that we can say that the class of “classes not members of themselves” is necessarily not a member of itself, without this giving rise to a contradiction. I resolve the barber paradox differently, by saying that, unlike all other men in town, the barber can well both shave himself and be shaved by the barber (himself). In the Russell paradox, one of the conflicting classes is wholly eliminated. In the barber paradox, the conflict between the classes is softened in a single case (that of the barber himself). Since the two paradoxes are not resolved in the same way, they must be regarded as logically distinct.
From Topics (published only online so far).
[1] Quotation from Principia Mathematica by Nicholas Rescher in Paradoxes: Their Roots, Range, and Resolution, p. 172. This “Vicious Circle Principle” was earlier formulated by Henri Poincaré.
[2] Alternatively, if the latter is thought to be problematic, then the former cannot be thought so. In any case, one of the two has to be unproblematic, for discourse to be at all possible. I mention this alternative, only because at first sight it may seem that the negative term “all classes not members of themselves” is the problematic one, since it apparently results in paradox (whereas the positive one apparently does not). In truth, this negative term is unproblematic, and it is the positive term “all classes members of themselves” which causes the paradox. Note this well.
[3] I will not here get into a detailed analysis of this theory. I refer readers to my previous, more detailed analyses in my books Future Logic (chapters 43-45) and A Fortiori Logic (Appendix 7.5).
[4] I refer readers to the excellent exposition and critique of Russell’s paradox and his attempted resolutions of it, in William and Martha Kneales’ The Development of Logic, chapter 11.
[5] Op. cit. pp. 172-73. While this SIP principle is intuitively sound, and relevant to the case at hand, it must be said that it is not a general truth. In truth, much of human discourse is made through more or less vague terms. Relatively few terms, if any, are fully and finally defined. This is because our knowledge is essentially inductive, rather than (as many logicians imagine) deductive. We use a word (when we need one) and a working definition (when we have one) as pragmatic tools. Our understanding of their reference is at all times tentative and temporary. As our knowledge grows and our analyses are refined, our terms (hopefully) gain increasing accuracy, become more pointed. So, the principle here proposed by Rescher should not be taken too generally. Meaningful discussion occurs all the time with imperfectly defined words; that is the norm rather than the exception, and we usually manage very well to avoid contradictions nonetheless. Meaning is not essentially a verbal issue, but one of insight and understanding.
[6] The Development of Logic, p. 655.